Ejercicios Aplicaciones Cuadricas y Cónicas

Ejercicios

Cónicas

http://ocw.unizar.es/ocw/pluginfile.php/72/mod_label/intro/u5conreto.pdf

http://www2.uah.es/josemsalazar/material_docente_arquitectura/alg/Conicas_y_cuadricas/ejconicas_enunc.pdf

http://www2.uah.es/josemsalazar/material_docente_arquitectura/alg/Conicas_y_cuadricas/ejerc_conicas_resueltos.pdf

Cuadricas

http://www2.uah.es/josemsalazar/material_docente_arquitectura/alg/Conicas_y_cuadricas/cuadricas_-_copia_enunc.pdf

http://www2.uah.es/josemsalazar/material_docente_arquitectura/alg/Conicas_y_cuadricas/cuadricas_-_copia.pdf

Cónicas y Cuadricas (Imágenes, Formulas, Tablas)

Aplicaciones Cónicas 

La ecuación general de una cónica es 

O en otros términos 

     Entre los tipos que podemos encontrar de cónicas podemos destacar las parábolas, elipses, e hipérbolas. Estas cónicas se denominan no degeneradas.

Parábola

     La Parábola es el lugar geométrico de los puntos del plano que están a una misma distancia de un punto dado F llamado foco y de una recta dada l llamada directriz.

Antena parabólica

Elementos de una parábola

Estructura con forma de Parábola

Montana Rusa con forma parabólica

• DIRECTRIZ: Es la recta sobre la cual si medimos su distancia hasta un punto cualquiera de la parábola,esta debe ser igual a la distancia de este mismo punto al Foco.
• EJE FOCAL: Es la recta perpendicular a la directriz que pasa por el Foco.
• VÉRTICE: Es el punto por en el cual la parábola corta al eje focal.
• LADO RECTO: Es un segmento paralelo a la directriz, que pasa por el foco y es perpendicular al eje focal y sus extremos son puntos de la parábola (A,B).
• PARÁMETRO: La distancia entre el vértice y la directriz que es la misma entre el vértice y el foco de una parábola es lo que recibe el nombre de parábola y denotamos con la letra p.

Elipse

En este tobogán se observa una Elipse

Que es ?            

• Es el lugar geométrico de los puntos de un plano tales que la suma de las distancias a dos puntos dados de dicho plano,llamados focos,es constante.
• También es la curva simétrica cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría-con angulo mayor que el de la generatriz respecto del eje de revolución.Una elipse que gira alrededor de su eje menor genera un esferoide achatado,mientras que una elipse que gira alrededor de su eje principal genera un esferoide alargado.

   Elementos del elipse

La elipse es una curva plana y cerrada, simétrica con respecto a dos ejes perpendiculares entre si:

• EL SEMIEJE MAYOR: El segmento C-a de la figura.
•  EL SEMIEJE MENOR: El segmento C-b de la figura.
•  

Observamos una Elipse en un anuncio

 Sabias Que?  

• La Elipse como curva geométrica fue estudiada por Menecmo,investigada por Euclides, y su nombre se atribuye a Apolonio de Perge.
•  El foco y la directriz sección cónica de una elipse fueron estudiadas por Poppus.
•  En 1602 Kepler creia que la orbita de Marte era ovalada aunque mas tarde descubrio que se trataba de una elipse con el Sol en un foco.De hecho, Kepler  introdujo la palabra "focus" y publico se descubrimiento en 1609.
•  Halley,en 1705, demostro que el cometa que ahora lleva su nombre trazaba una orbita eliptica alrededor del Sol.  

circunferencia

Como la definimos: Es una linea curva,plana y cerrada,cuya definición mas usual es:

En el logo de este C. Comercial encontramos una circunferencia

La circunferencia:  Es el lugar geométrico de los puntos del plano que están a una distancia r de otro punto dado C.r es radio de la circunferencia y el punto C es el centro de la misma.

      También   a  la distancia entre cualquiera de sus puntos y el centro se le denomina radio. El segmento de recta formado por dos radios alineados se llama diámetro. Es la mayor distancia posible entre dos puntos que pertenezcan a la circunferencia. La longitud del diámetro es el doble de la longitud del radio. La circunferencia sólo posee longitud. Se distingue del círculo en que éste es el lugar geométrico de los puntos contenidos en una circunferencia determinada; es decir, la circunferencia es el perímetro del círculo cuya superficie contiene.

En este Bold se aprecia una circunferencia

   Puede ser considerada como una elipse de excentricidad nula, o una elipse cuyos semiejes son iguales. También se puede describir como la sección, perpendicular al eje, de una superficie cónica o cilíndrica, o como un polígono de infinitos lados, cuya apotema coincide con su radio.

Hipérbola

     Una hipérbola es una sección cónica,una curva abierta de dos ramas obtenida al cortar un cono recto por uno oblicuo al eje de simetría con angulo menor que el de la generatriz respecto al eje de revolución.

En el reflejo de esta lampara se hace una hipérbola

• Una HIPÉRBOLA es el lugar geométrico de los puntos del plano que cumplan con la condición de que el valor absoluto de la diferencia de distancias a dos puntos fijos, F y F', llamados focos( son dos puntos. Respecto del foco, cada punto de la parábola posee la misma distancia que hasta una recta llamada directriz.) de la hipérbola, es una constante positiva.La Hipérbola consta de dos ramas diferentes,cada una de longitud infinita.

                            

Elementos de la hipérbola

• FOCOS: Son los puntos fijos F Y F'.
• EJE FOCAL: Es la recta que pasa por los focos.
• EFE SECUNDARIO O IMAGINARIO: Es la mediatriz del segmento  .
• CENTRO: Es el punto de intersección de los ejes.
• VÉRTICES: Los puntos A y A' son los puntos de intersección de la hipérbola con el eje focal.
• RADIOS VECTORES: Son los segmentos que van desde un punto de la hipérbola hasta los focos: PF y PF'.
• DISTANCIA FOCAL: Es el segmento    de longitud 2c.
• EJE MAYOR: Es el segmento    de longitud 2a.
• EJE MENOR: Es el segmento    de longitud 2b.
• EJE DE SIMETRÍA: Son las rectas que contienen al eje real o al eje imaginario.
• ASÍNTOTAS: Son las rectas de ecuaciones  : 

Aplicaciones Cuádricas

La ecuación general de una cuádrica es 

En términos matriciales 

       

       Entre los tipos que podemos encontrar de cuádricas podemos destacar los paraboloides, elipsoides, e hiperboloides. Estas son cuádricas no degeneradas.

Aplicaciones Cónicas y Cuádricas (TEORÍA)

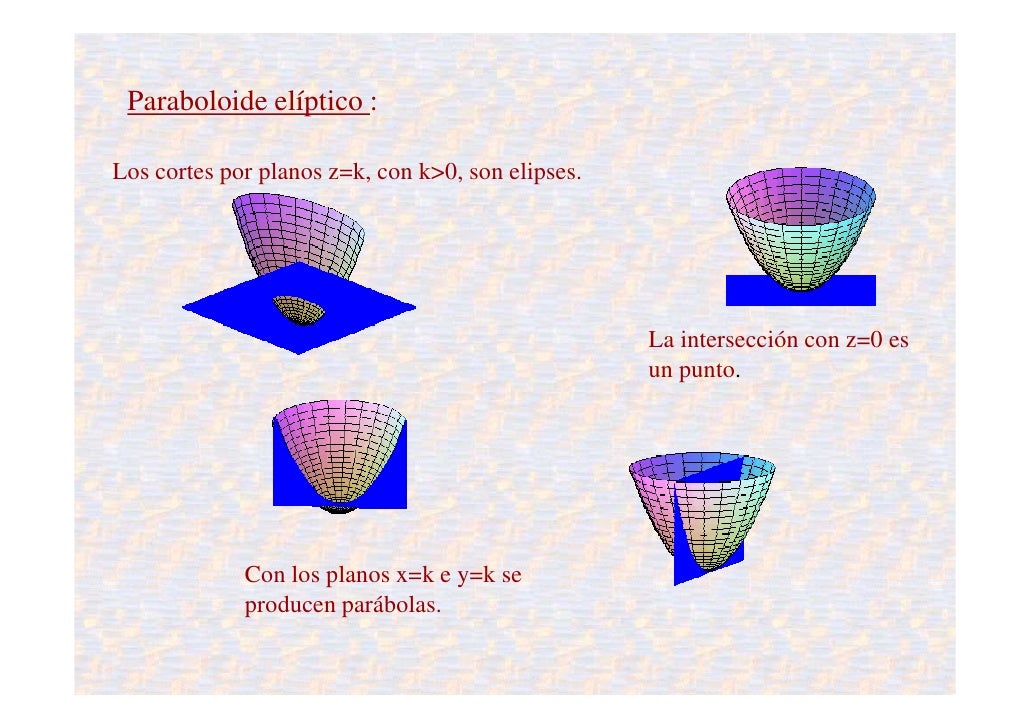
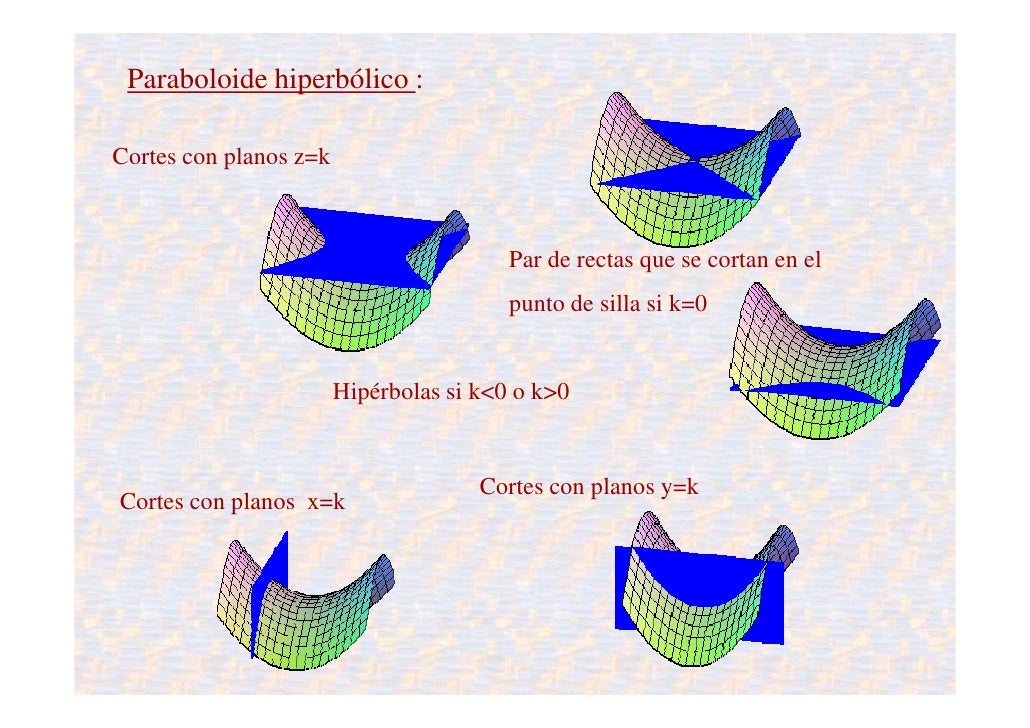
cónicas

     Cuando nos referimos a las cónicas, usualmente pensamos solo en la parte matemática, vale decir, las ecuaciones y los conceptos de éstas. Sin embargo, desde los tiempos antiguos tenían utilidades prácticas (ya sea medio legendarios como la hazaña de Arquímedes, al destruir naves romanas con un espejo gigante o reales, como la creación de espejos pequeños, importantes más adelante en la óptica).

    En la Edad Moderna y Contemporánea, adquirieron mayor relevancia para el ser humano en ámbitos tanto matemáticos como físicos, inclusive llegando más allá, sobrepasando las expectativas que se tenían, como el uso en telecomunicaciones e industria.

   Quizá, cuando la tecnología siga avanzando tal como lo hace ahora en el siglo XXI, tendremos que recurrir a las ideas de las cónicas, con propósito de mejorar lo preexistente.

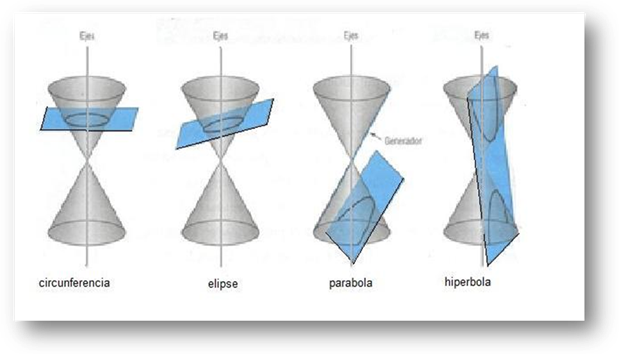
     También se conoce como Cónica que es cada una de las curvas planas que se obtienen al cortar una superficie cónica por un plano que no pasa por su vértice.

     Existen 4 tipos de ejemplos de intersección de un plano en un cono los cuales son: 

• Hipérbola
• Parábola 
• Elipse 
• Circunferencia 

Aplicaciones cónicas

      Las cónicas poseen curiosas e interesantes propiedades por las que resultan sumamente útiles en la naturaleza, la ciencia, la técnica o el arte. Por ejemplo, las órbitas de los planetas y cometas en su rotación alrededor del Sol son cónicas; los faros de los coches tienen sección parabólica, al igual que los hornos solares y las antenas de seguimiento de satélites, debido a que en la parábola los rayos que pasan por el foco salen paralelos al eje y viceversa. También existe un tipo de ayuda a la navegación (loran) basado en las propiedades de las hipérbolas.

Hipérbola 

      Una hipérbola es una sección cónica, una curva de dos ramas obtenida al cortar un cono recto por un plano oblicuo al eje de simetría –con ángulo menor que el de la generatriz respecto del eje de revolución.
Se define también como el lugar geométrico de los puntos cuya diferencia de distancias a dos puntos fijos, llamados focos, es constante.

Elipse

      La elipse es el lugar geométrico de los puntos del plano tales que la suma de las distancias a dos puntos fijos llamados focos es constante.

      Una elipse es la curva cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría –con ángulo mayor que el de la generatriz respecto del eje de revolución.

Parábola 

      La parábola es una sección cónica generada al cortar un cono recto con un plano paralelo a la directriz.

      Se define también como el lugar geométrico de los puntos que equidistan de una recta (eje o directriz) y un punto fijo llamado foco.
La parábola aparece en muchas ramas de las ciencias aplicadas, debido a que las gráficas de ecuaciones cuadráticas son parábolas. Por ejemplo, la trayectoria ideal del movimiento de los cuerpos bajo la influencia de la gravedad.

Circunferencia

      Una circunferencia es el lugar geométrico de los puntos del plano equidistantes de otro fijo, llamado centro; esta distancia se denomina radio. Sólo posee longitud. Se distingue del círculo en que este es el lugar geométrico de los puntos contenidos en una circunferencia determinada, es decir, la circunferencia es el perímetro del círculo cuya superficie contiene.

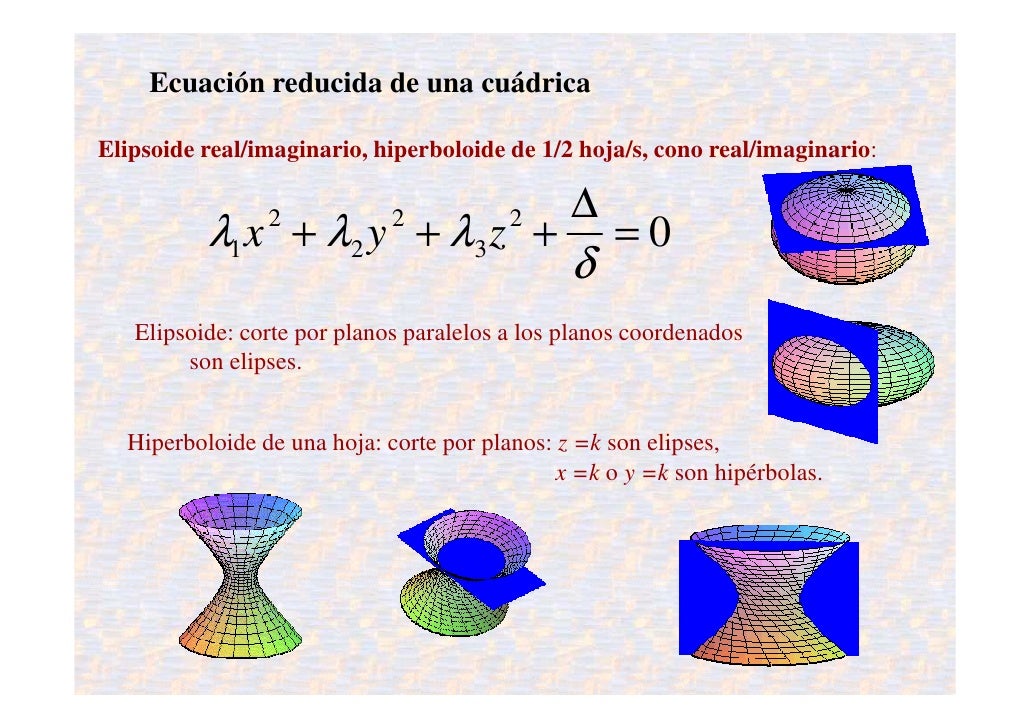
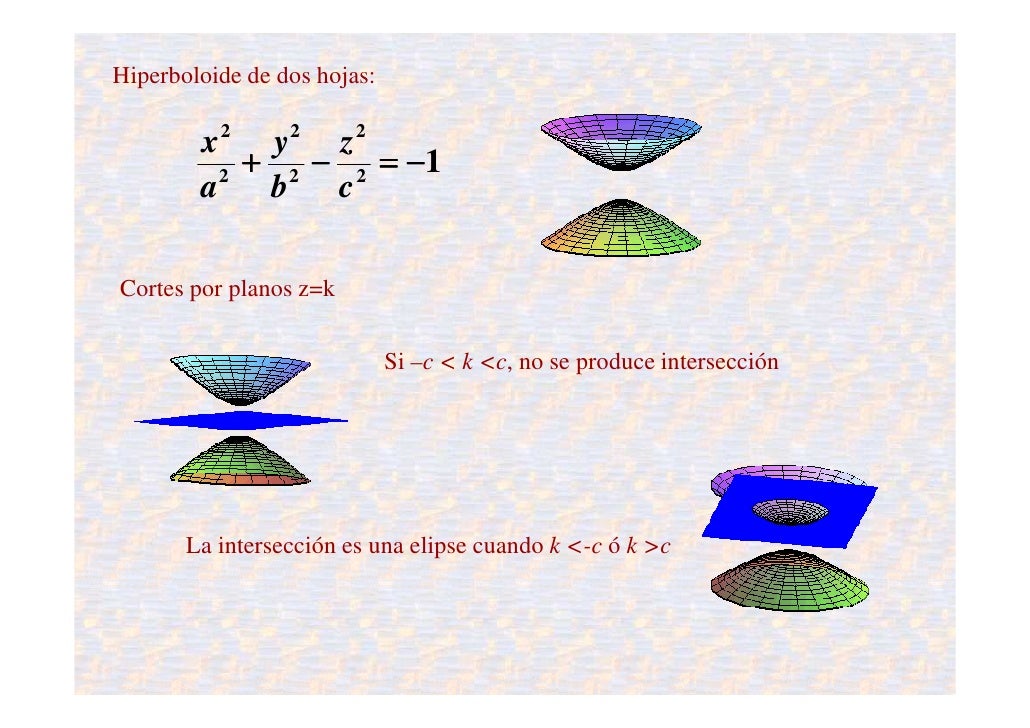
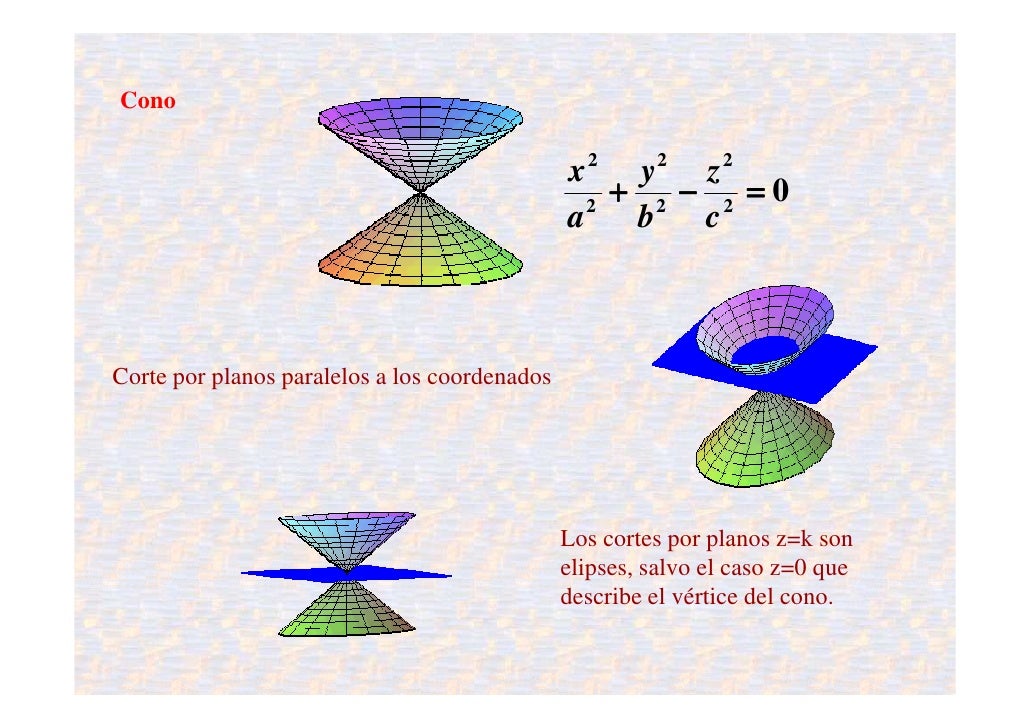
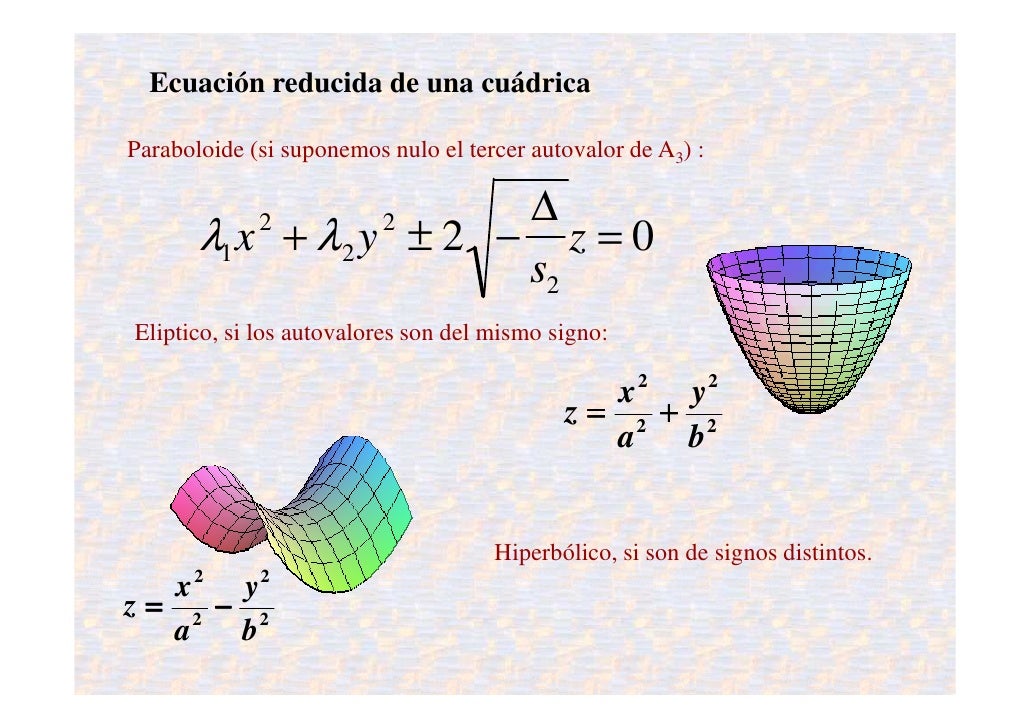
Cuádrica 

Una cuádrica es el lugar geométrico de los puntos del espacio (x,y,z) que verifican una ecuación de segundo grado del tipo:

Clasificación

     Las cuádricas se clasifican de acuerdo a su signatura , es decir, el módulo de la diferencia entre el número de auto valores positivos y negativos de A₀₀. Sin embargo, para calcular la signatura de la cuádrica no es necesario diagonalizar la matriz, debido a la existencia de unas cantidades invariantes asociadas a A₀₀ que permiten determinar  sin necesidad de calcular explícitamente sus auto valores.